12 Statistical learning
Prerequisites
This chapter assumes proficiency with geographic data analysis, for example gained by studying the contents and working-through the exercises in Chapters 2 to 7. A familiarity with generalized linear models (GLM) and machine learning is highly recommended (for example from A. Zuur et al. 2009; James et al. 2013).
The chapter uses the following packages:85
library(sf)
library(terra)
library(dplyr)
library(future) # parallel processing
library(lgr) # logging framework for R
library(mlr3) # unified interface to machine learning algorithms
library(mlr3learners) # most important machine learning algorithms
library(mlr3extralearners) # access to even more learning algorithms
library(mlr3spatiotempcv) # spatio-temporal resampling strategies
library(mlr3tuning) # hyperparameter tuning
library(mlr3viz) # plotting functions for mlr3 objects
library(progressr) # report progress updatesRequired data will be attached in due course.
12.1 Introduction
Statistical learning is concerned with the use of statistical and computational models for identifying patterns in data and predicting from these patterns. Due to its origins, statistical learning is one of R’s great strengths (see Section 1.3).86 Statistical learning combines methods from statistics and machine learning and can be categorized into supervised and unsupervised techniques. Both are increasingly used in disciplines ranging from physics, biology and ecology to geography and economics (James et al. 2013).
This chapter focuses on supervised techniques in which there is a training dataset, as opposed to unsupervised techniques such as clustering. Response variables can be binary (such as landslide occurrence), categorical (land use), integer (species richness count) or numeric (soil acidity measured in pH). Supervised techniques model the relationship between such responses — which are known for a sample of observations — and one or more predictors.
The primary aim of much machine learning research is to make good predictions. Machine learning thrives in the age of ‘big data’ because its methods make few assumptions about input variables and can handle huge datasets. Machine learning is conducive to tasks such as the prediction of future customer behavior, recommendation services (music, movies, what to buy next), face recognition, autonomous driving, text classification and predictive maintenance (infrastructure, industry).
This chapter is based on a case study: modeling the occurrence of landslides. This application links to the applied nature of geocomputation, defined in Chapter 1, and illustrates how machine learning borrows from the field of statistics when the sole aim is prediction. Therefore, this chapter first introduces modeling and cross-validation concepts with the help of a Generalized Linear Model (A. Zuur et al. 2009). Building on this, the chapter implements a more typical machine learning algorithm, namely a Support Vector Machine (SVM). The models’ predictive performance will be assessed using spatial cross-validation (CV), which accounts for the fact that geographic data is special.
CV determines a model’s ability to generalize to new data, by splitting a dataset (repeatedly) into training and test sets. It uses the training data to fit the model, and checks its performance when predicting against the test data. CV helps to detect overfitting since models that predict the training data too closely (noise) will tend to perform poorly on the test data.
Randomly splitting spatial data can lead to training points that are neighbors in space with test points. Due to spatial autocorrelation, test and training datasets would not be independent in this scenario, with the consequence that CV fails to detect a possible overfitting. Spatial CV alleviates this problem and is the central theme in this chapter.
Hence, and to emphasize it again, this chapter is focusing on the predictive performance of models. It does not teach how to do predictive mapping. This will be the topic of Chapter 15.
12.2 Case study: Landslide susceptibility
This case study is based on a dataset of landslide locations in Southern Ecuador, illustrated in Figure 12.1 and described in detail in Muenchow, Brenning, and Richter (2012). A subset of the dataset used in that paper is provided in the spDataLarge package, which can be loaded as follows:
data("lsl", "study_mask", package = "spDataLarge")
ta = terra::rast(system.file("raster/ta.tif", package = "spDataLarge"))The above code loads three objects: a data.frame named lsl, an sf object named study_mask and a SpatRaster (see Section 2.3.4) named ta containing terrain attribute rasters.
lsl contains a factor column lslpts where TRUE corresponds to an observed landslide ‘initiation point’, with the coordinates stored in columns x and y.87
There are 175 landslide and 175 non-landslide points, as shown by summary(lsl$lslpts).
The 175 non-landslide points were sampled randomly from the study area, with the restriction that they must fall outside a small buffer around the landslide polygons.

FIGURE 12.1: Landslide initiation points (red) and points unaffected by landsliding (blue) in Southern Ecuador.
The first three rows of lsl, rounded to two significant digits, can be found in Table 12.1.
| x | y | lslpts | slope | cplan | cprof | elev | log10_carea | |
|---|---|---|---|---|---|---|---|---|
| 1 | 713888 | 9558537 | FALSE | 34 | 0.023 | 0.003 | 2400 | 2.8 |
| 2 | 712788 | 9558917 | FALSE | 39 | -0.039 | -0.017 | 2100 | 4.1 |
| 350 | 713826 | 9559078 | TRUE | 35 | 0.020 | -0.003 | 2400 | 3.2 |
To model landslide susceptibility, we need some predictors.
Since terrain attributes are frequently associated with landsliding (Muenchow, Brenning, and Richter 2012), we have already extracted following terrain attributes from ta to lsl:
-
slope: slope angle (°) -
cplan: plan curvature (rad m−1) expressing the convergence or divergence of a slope and thus water flow -
cprof: profile curvature (rad m-1) as a measure of flow acceleration, also known as downslope change in slope angle -
elev: elevation (m a.s.l.) as the representation of different altitudinal zones of vegetation and precipitation in the study area -
log10_carea: the decadic logarithm of the catchment area (log10 m2) representing the amount of water flowing towards a location
It might be a worthwhile exercise to compute the terrain attributes with the help of R-GIS bridges (see Chapter 10) and extract them to the landslide points (see Exercise section at the end of this chapter).
12.3 Conventional modeling approach in R
Before introducing the mlr3 package, an umbrella-package providing a unified interface to dozens of learning algorithms (Section 12.5), it is worth taking a look at the conventional modeling interface in R. This introduction to supervised statistical learning provides the basis for doing spatial CV, and contributes to a better grasp on the mlr3 approach presented subsequently.
Supervised learning involves predicting a response variable as a function of predictors (Section 12.4).
In R, modeling functions are usually specified using formulas (see ?formula for more details on R formulas).
The following command specifies and runs a generalized linear model:
It is worth understanding each of the three input arguments:
- A formula, which specifies landslide occurrence (
lslpts) as a function of the predictors - A family, which specifies the type of model, in this case
binomialbecause the response is binary (see?family) - The data frame which contains the response and the predictors (as columns)
The results of this model can be printed as follows (summary(fit) provides a more detailed account of the results):
class(fit)
#> [1] "glm" "lm"
fit
#>
#> Call: glm(formula = lslpts ~ slope + cplan + cprof + elev + log10_carea,
#> family = binomial(), data = lsl)
#>
#> Coefficients:
#> (Intercept) slope cplan cprof elev log10_carea
#> 2.51e+00 7.90e-02 -2.89e+01 -1.76e+01 1.79e-04 -2.27e+00
#>
#> Degrees of Freedom: 349 Total (i.e. Null); 344 Residual
#> Null Deviance: 485
#> Residual Deviance: 373 AIC: 385The model object fit, of class glm, contains the coefficients defining the fitted relationship between response and predictors.
It can also be used for prediction.
This is done with the generic predict() method, which in this case calls the function predict.glm().
Setting type to response returns the predicted probabilities (of landslide occurrence) for each observation in lsl, as illustrated below (see ?predict.glm).
pred_glm = predict(object = fit, type = "response")
head(pred_glm)
#> 1 2 3 4 5 6
#> 0.1901 0.1172 0.0952 0.2503 0.3382 0.1575Spatial distribution maps can be made by applying the coefficients to the predictor rasters.
This can be done manually or with terra::predict().
In addition to a model object (fit), the latter function also expects a SpatRaster with the predictors (raster layers) named as in the model’s input data frame (Figure 12.2).
# making the prediction
pred = terra::predict(ta, model = fit, type = "response")
FIGURE 12.2: Spatial distribution mapping of landslide susceptibility using a GLM.
Here, when making predictions we neglect spatial autocorrelation since we assume that on average the predictive accuracy remains the same with or without spatial autocorrelation structures. However, it is possible to include spatial autocorrelation structures into models as well as into predictions. Though, this is beyond the scope of this book, we give the interested reader some pointers where to look it up:
- The predictions of regression kriging combines the predictions of a regression with the kriging of the regression’s residuals (Goovaerts 1997; Hengl 2007; Bivand, Pebesma, and Gómez-Rubio 2013).
- One can also add a spatial correlation (dependency) structure to a generalized least squares model (
nlme::gls(); A. Zuur et al. (2009); A. F. Zuur et al. (2017)).
- One can also use mixed-effect modeling approaches. Basically, a random effect imposes a dependency structure on the response variable which in turn allows for observations of one class to be more similar to each other than to those of another class (A. Zuur et al. 2009). Classes can be, for example, bee hives, owl nests, vegetation transects or an altitudinal stratification. This mixed modeling approach assumes normal and independent distributed random intercepts. This can even be extended by using a random intercept that is normal and spatially dependent. For this, however, you will have to resort most likely to Bayesian modeling approaches since frequentist software tools are rather limited in this respect especially for more complex models (Blangiardo and Cameletti 2015; A. F. Zuur et al. 2017).
Spatial distribution mapping is one very important outcome of a model (Figure 12.2).
Even more important is how good the underlying model is at making them since a prediction map is useless if the model’s predictive performance is bad.
One of the most popular measures to assess the predictive performance of a binomial model is the Area Under the Receiver Operator Characteristic Curve (AUROC).
This is a value between 0.5 and 1.0, with 0.5 indicating a model that is no better than random and 1.0 indicating perfect prediction of the two classes.
Thus, the higher the AUROC, the better the model’s predictive power.
The following code chunk computes the AUROC value of the model with roc(), which takes the response and the predicted values as inputs.
auc() returns the area under the curve.
An AUROC value of 0.82 represents a good fit. However, this is an overoptimistic estimation since we have computed it on the complete dataset. To derive a biased-reduced assessment, we have to use cross-validation and in the case of spatial data should make use of spatial CV.
12.4 Introduction to (spatial) cross-validation
Cross-validation belongs to the family of resampling methods (James et al. 2013). The basic idea is to split (repeatedly) a dataset into training and test sets whereby the training data is used to fit a model which then is applied to the test set. Comparing the predicted values with the known response values from the test set (using a performance measure such as the AUROC in the binomial case) gives a bias-reduced assessment of the model’s capability to generalize the learned relationship to independent data. For example, a 100-repeated 5-fold cross-validation means to randomly split the data into five partitions (folds) with each fold being used once as a test set (see upper row of Figure 12.3). This guarantees that each observation is used once in one of the test sets, and requires the fitting of five models. Subsequently, this procedure is repeated 100 times. Of course, the data splitting will differ in each repetition. Overall, this sums up to 500 models, whereas the mean performance measure (AUROC) of all models is the model’s overall predictive power.
However, geographic data is special. As we will see in Chapter 13, the ‘first law’ of geography states that points close to each other are, generally, more similar than points further away (Miller 2004). This means these points are not statistically independent because training and test points in conventional CV are often too close to each other (see first row of Figure 12.3). ‘Training’ observations near the ‘test’ observations can provide a kind of ‘sneak preview’: information that should be unavailable to the training dataset. To alleviate this problem ‘spatial partitioning’ is used to split the observations into spatially disjointed subsets (using the observations’ coordinates in a k-means clustering; Brenning (2012b); second row of Figure 12.3). This partitioning strategy is the only difference between spatial and conventional CV. As a result, spatial CV leads to a bias-reduced assessment of a model’s predictive performance, and hence helps to avoid overfitting.

FIGURE 12.3: Spatial visualization of selected test and training observations for cross-validation of one repetition. Random (upper row) and spatial partitioning (lower row).
12.5 Spatial CV with mlr3
There are dozens of packages for statistical learning, as described for example in the CRAN machine learning task view. Getting acquainted with each of these packages, including how to undertake cross-validation and hyperparameter tuning, can be a time-consuming process. Comparing model results from different packages can be even more laborious. The mlr3 package and ecosystem was developed to address these issues. It acts as a ‘meta-package’, providing a unified interface to popular supervised and unsupervised statistical learning techniques including classification, regression, survival analysis and clustering (Lang et al. 2019; Becker et al. 2022). The standardized mlr3 interface is based on eight ‘building blocks’. As illustrated in Figure 12.4, these have a clear order.

FIGURE 12.4: Basic building blocks of the mlr3 package. Source: Becker et al. (2022). (Permission to reuse this figure was kindly granted.)
The mlr3 modeling process consists of three main stages. First, a task specifies the data (including response and predictor variables) and the model type (such as regression or classification). Second, a learner defines the specific learning algorithm that is applied to the created task. Third, the resampling approach assesses the predictive performance of the model, i.e., its ability to generalize to new data (see also Section 12.4).
12.5.1 Generalized linear model
To use a GLM in mlr3, we must create a task containing the landslide data.
Since the response is binary (two-category variable) and has a spatial dimension, we create a classification task with as_task_classif_st() of the mlr3spatiotempcv package (Schratz et al. 2021, for non-spatial tasks, use mlr3::as_task_classif() or mlr3::as_task_regr() for regression tasks, see ?Task for other task types).88
The first essential argument of these as_task_ functions is x.
x expects that the input data includes the response and predictor variables.
The target argument indicates the name of a response variable (in our case this is lslpts) and positive determines which of the two factor levels of the response variable indicate the landslide initiation point (in our case this is TRUE).
All other variables of the lsl dataset will serve as predictors.
For spatial CV, we need to provide a few extra arguments.
The coordinate_names argument expects the names of the coordinate columns (see Section 12.4 and Figure 12.3).
Additionally, we should indicate the used CRS (crs) and decide if we want to use the coordinates as predictors in the modeling (coords_as_features).
# 1. create task
task = mlr3spatiotempcv::as_task_classif_st(
mlr3::as_data_backend(lsl),
target = "lslpts",
id = "ecuador_lsl",
positive = "TRUE",
coordinate_names = c("x", "y"),
crs = "EPSG:32717",
coords_as_features = FALSE
)Note that mlr3spatiotempcv::as_task_classif_st() also accepts an sf-object as input for the backend parameter.
In this case, you might only want to additionally specify the coords_as_features argument.
We did not convert lsl into an sf-object because as_task_classif_st() would just turn it back into a non-spatial data.table object in the background.
For a short data exploration, the autoplot() function of the mlr3viz package might come in handy since it plots the response against all predictors and all predictors against all predictors (not shown).
# plot response against each predictor
mlr3viz::autoplot(task, type = "duo")
# plot all variables against each other
mlr3viz::autoplot(task, type = "pairs")Having created a task, we need to choose a learner that determines the statistical learning method to use.
All classification learners start with classif. and all regression learners with regr. (see ?Learner for details).
mlr3extralearners::list_mlr3learners() lists all available learners and from which package mlr3 imports them (Table 12.3).
To find out about learners that are able to model a binary response variable, we can run:
mlr3extralearners::list_mlr3learners(
filter = list(class = "classif", properties = "twoclass"),
select = c("id", "mlr3_package", "required_packages")) |>
head()| Class | Name | Short name | Package |
|---|---|---|---|
| classif.adaboostm1 | ada Boosting M1 | adaboostm1 | RWeka |
| classif.binomial | Binomial Regression | binomial | stats |
| classif.featureless | Featureless classifier | featureless | mlr |
| classif.fnn | Fast k-Nearest Neighbour | fnn | FNN |
| classif.gausspr | Gaussian Processes | gausspr | kernlab |
| classif.IBk | k-Nearest Neighbours | ibk | RWeka |
This yields all learners able to model two-class problems (landslide yes or no).
We opt for the binomial classification method used in Section 12.3 and implemented as classif.log_reg in mlr3learners.
Additionally, we need to specify the predict.type which determines the type of the prediction with prob resulting in the predicted probability for landslide occurrence between 0 and 1 (this corresponds to type = response in predict.glm()).
# 2. specify learner
learner = mlr3::lrn("classif.log_reg", predict_type = "prob")To access the help page of the learner and find out from which package it was taken, we can run:
learner$help()The set-up steps for modeling with mlr3 may seem tedious.
But remember, this single interface provides access to the 130+ learners shown by mlr3extralearners::list_mlr3learners(); it would be far more tedious to learn the interface for each learner!
Further advantages are simple parallelization of resampling techniques and the ability to tune machine learning hyperparameters (see Section 12.5.2).
Most importantly, (spatial) resampling in mlr3spatiotempcv (Schratz et al. 2021) is straightforward, requiring only two more steps: specifying a resampling method and running it.
We will use a 100-repeated 5-fold spatial CV: five partitions will be chosen based on the provided coordinates in our task and the partitioning will be repeated 100 times:89
# 3. specify resampling
resampling = mlr3::rsmp("repeated_spcv_coords", folds = 5, repeats = 100)To execute the spatial resampling, we run resample() using the previously specified task, learner, and resampling strategy.
This takes some time (around 15 seconds on a modern laptop) because it computes 500 resampling partitions and 500 models.
As performance measure, we again choose the AUROC.
To retrieve it, we use the score() method of the resampling result output object (score_spcv_glm).
This returns a data.table object with 500 rows – one for each model.
# reduce verbosity
lgr::get_logger("mlr3")$set_threshold("warn")
# run spatial cross-validation and save it to resample result glm (rr_glm)
rr_spcv_glm = mlr3::resample(task = task,
learner = learner,
resampling = resampling)
# compute the AUROC as a data.table
score_spcv_glm = rr_spcv_glm$score(measure = mlr3::msr("classif.auc"))
# keep only the columns you need
score_spcv_glm = dplyr::select(score_spcv_glm, task_id, learner_id,
resampling_id, classif.auc)The output of the preceding code chunk is a bias-reduced assessment of the model’s predictive performance.
We have saved it as extdata/12-bmr_score.rds in the book’s GitHub repository.
If required, you can read it in as follows:
score = readRDS("extdata/12-bmr_score.rds")
score_spcv_glm = dplyr::filter(score, learner_id == "classif.log_reg",
resampling_id == "repeated_spcv_coords")To compute the mean AUROC over all 500 models, we run:
To put these results in perspective, let us compare them with AUROC values from a 100-repeated 5-fold non-spatial cross-validation (Figure 12.5; the code for the non-spatial cross-validation is not shown here but will be explored in the exercise section). As expected (see Section 12.4), the spatially cross-validated result yields lower AUROC values on average than the conventional cross-validation approach, underlining the over-optimistic predictive performance of the latter due to its spatial autocorrelation.
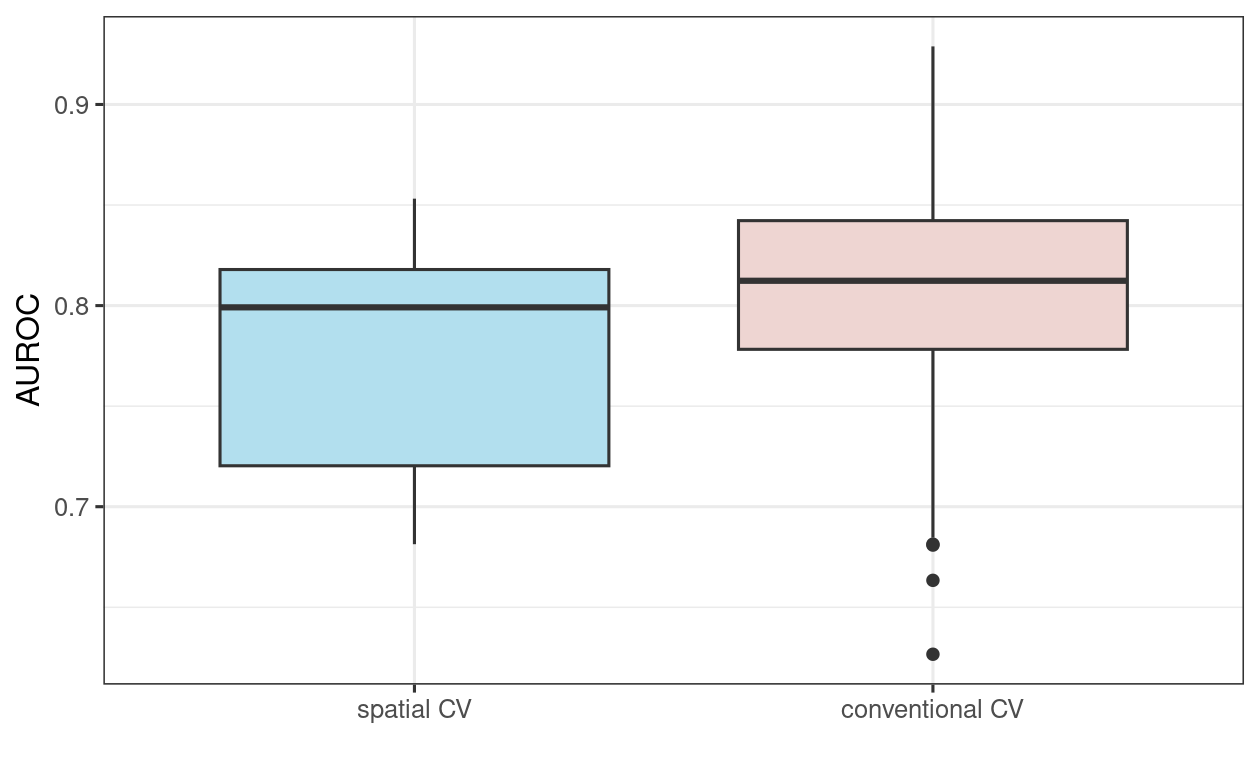
FIGURE 12.5: Boxplot showing the difference in GLM AUROC values on spatial and conventional 100-repeated 5-fold cross-validation.
12.5.2 Spatial tuning of machine-learning hyperparameters
Section 12.4 introduced machine learning as part of statistical learning. To recap, we adhere to the following definition of machine learning by Jason Brownlee:
Machine learning, more specifically the field of predictive modeling, is primarily concerned with minimizing the error of a model or making the most accurate predictions possible, at the expense of explainability. In applied machine learning we will borrow, reuse and steal algorithms from many different fields, including statistics and use them towards these ends.
In Section 12.5.1 a GLM was used to predict landslide susceptibility. This section introduces support vector machines (SVM) for the same purpose. Random forest models might be more popular than SVMs; however, the positive effect of tuning hyperparameters on model performance is much more pronounced in the case of SVMs (Probst, Wright, and Boulesteix 2018). Since (spatial) hyperparameter tuning is the major aim of this section, we will use an SVM. For those wishing to apply a random forest model, we recommend to read this chapter, and then proceed to Chapter 15 in which we will apply the currently covered concepts and techniques to make spatial distribution maps based on a random forest model.
SVMs search for the best possible ‘hyperplanes’ to separate classes (in a classification case) and estimate ‘kernels’ with specific hyperparameters to create non-linear boundaries between classes (James et al. 2013). Machine learning algorithms often feature hyperparameters and parameters. Parameters can be estimated from the data while hyperparameters are set before the learning begins (see also the machine mastery blog and the hyperparameter optimization chapter of the mlr3 book). The optimal hyperparameter configuration is usually found within a specific search space and determined with the help of cross-validation methods. This is called hyperparameter tuning and the main topic of this section.
Some SVM implementations such as that provided by kernlab allow hyperparameters to be tuned automatically, usually based on random sampling (see upper row of Figure 12.3). This works for non-spatial data but is of less use for spatial data where ‘spatial tuning’ should be undertaken.
Before defining spatial tuning, we will set up the mlr3 building blocks, introduced in Section 12.5.1, for the SVM.
The classification task remains the same, hence we can simply reuse the task object created in Section 12.5.1.
Learners implementing SVM can be found using the list_mlr3learners() command of the mlr3extralearners.
Of the options, we will use ksvm() from the kernlab package (Karatzoglou et al. 2004).
To allow for non-linear relationships, we use the popular radial basis function (or Gaussian) kernel ("rbfdot") which is also the default of ksvm().
Setting the type argument to "C-svc" makes sure that ksvm() is solving a classification task.
To make sure that the tuning does not stop because of one failing model, we additionally define a fallback learner (for more information please refer to https://mlr3book.mlr-org.com/chapters/chapter10/advanced_technical_aspects_of_mlr3.html#sec-fallback).
lrn_ksvm = mlr3::lrn("classif.ksvm", predict_type = "prob", kernel = "rbfdot",
type = "C-svc")
lrn_ksvm$fallback = lrn("classif.featureless", predict_type = "prob")The next stage is to specify a resampling strategy. Again we will use a 100-repeated 5-fold spatial CV.
# performance estimation level
perf_level = mlr3::rsmp("repeated_spcv_coords", folds = 5, repeats = 100)Note that this is the exact same code as used for the resampling for the GLM in Section 12.5.1; we have simply repeated it here as a reminder.
So far, the process has been identical to that described in Section 12.5.1. The next step is new, however: to tune the hyperparameters. Using the same data for the performance assessment and the tuning would potentially lead to overoptimistic results (Cawley and Talbot 2010). This can be avoided using nested spatial CV.

FIGURE 12.6: Schematic of hyperparameter tuning and performance estimation levels in CV. (Figure was taken from Schratz et al. (2019). Permission to reuse it was kindly granted.)
This means that we split each fold again into five spatially disjoint subfolds which are used to determine the optimal hyperparameters (tune_level object in the code chunk below; see Figure 12.6 for a visual representation).
The random selection of values C and Sigma is additionally restricted to a predefined tuning space (search_space object).
The range of the tuning space was chosen with values recommended in the literature (Schratz et al. 2019).
To find the optimal hyperparameter combination, we fit 50 models (terminator object in the code chunk below) in each of these subfolds with randomly selected values for the hyperparameters C and Sigma.
# five spatially disjoint partitions
tune_level = mlr3::rsmp("spcv_coords", folds = 5)
# define the outer limits of the randomly selected hyperparameters
search_space = paradox::ps(
C = paradox::p_dbl(lower = -12, upper = 15, trafo = function(x) 2^x),
sigma = paradox::p_dbl(lower = -15, upper = 6, trafo = function(x) 2^x)
)
# use 50 randomly selected hyperparameters
terminator = mlr3tuning::trm("evals", n_evals = 50)
tuner = mlr3tuning::tnr("random_search")The next stage is to modify the learner lrn_ksvm in accordance with all the characteristics defining the hyperparameter tuning with auto_tuner().
at_ksvm = mlr3tuning::auto_tuner(
learner = lrn_ksvm,
resampling = tune_level,
measure = mlr3::msr("classif.auc"),
search_space = search_space,
terminator = terminator,
tuner = tuner
)The tuning is now set-up to fit 250 models to determine optimal hyperparameters for one fold. Repeating this for each fold, we end up with 1,250 (250 * 5) models for each repetition. Repeated 100 times means fitting a total of 125,000 models to identify optimal hyperparameters (Figure 12.3). These are used in the performance estimation, which requires the fitting of another 500 models (5 folds * 100 repetitions; see Figure 12.3). To make the performance estimation processing chain even clearer, let us write down the commands we have given to the computer:
- Performance level (upper left part of Figure 12.6) - split the dataset into five spatially disjoint (outer) subfolds
- Tuning level (lower left part of Figure 12.6) - use the first fold of the performance level and split it again spatially into five (inner) subfolds for the hyperparameter tuning. Use the 50 randomly selected hyperparameters in each of these inner subfolds, i.e., fit 250 models
- Performance estimation - Use the best hyperparameter combination from the previous step (tuning level) and apply it to the first outer fold in the performance level to estimate the performance (AUROC)
- Repeat steps 2 and 3 for the remaining four outer folds
- Repeat steps 2 to 4, 100 times
The process of hyperparameter tuning and performance estimation is computationally intensive. To decrease model runtime, mlr3 offers the possibility to use parallelization with the help of the future package. Since we are about to run a nested cross-validation, we can decide if we would like to parallelize the inner or the outer loop (see lower left part of Figure 12.6). Since the former will run 125,000 models, whereas the latter only runs 500, it is quite obvious that we should parallelize the inner loop. To set up the parallelization of the inner loop, we run:
library(future)
# execute the outer loop sequentially and parallelize the inner loop
future::plan(list("sequential", "multisession"),
workers = floor(availableCores() / 2))Additionally, we instructed future to only use half instead of all available cores (default), a setting that allows possible other users to work on the same high performance computing cluster in case one is used.
Now we are set up for computing the nested spatial CV.
Specifying the resample() parameters follows the exact same procedure as presented when using a GLM, the only difference being the store_models and encapsulate arguments.
Setting the former to TRUE would allow the extraction of the hyperparameter tuning results which is important if we plan follow-up analyses on the tuning.
The latter ensures that the processing continues even if one of the models throws an error.
This avoids the process stopping just because of one failed model, which is desirable on large model runs.
Once the processing is completed, one can have a look at the failed models.
After the processing, it is good practice to explicitly stop the parallelization with future:::ClusterRegistry("stop").
Finally, we save the output object (result) to disk in case we would like to use it in another R session.
Before running the subsequent code, be aware that it is time-consuming since it will run the spatial cross-validation with 125,500 models.
It can easily run for half a day on a modern laptop.
Note that runtime depends on many aspects: CPU speed, the selected algorithm, the selected number of cores and the dataset.
progressr::with_progress(expr = {
rr_spcv_svm = mlr3::resample(task = task,
learner = at_ksvm,
# outer resampling (performance level)
resampling = perf_level,
store_models = FALSE,
encapsulate = "evaluate")
})
# stop parallelization
future:::ClusterRegistry("stop")
# compute the AUROC values
score_spcv_svm = rr_spcv_svm$score(measure = mlr3::msr("classif.auc"))
# keep only the columns you need
score_spcv_svm = dplyr::select(score_spcv_svm, task_id, learner_id,
resampling_id, classif.auc)In case you do not want to run the code locally, we have saved score_svm in the book’s GitHub repository. They can be loaded as follows:
score = readRDS("extdata/12-bmr_score.rds")
score_spcv_svm = dplyr::filter(score, learner_id == "classif.ksvm.tuned",
resampling_id == "repeated_spcv_coords")Let us have a look at the final AUROC: the model’s ability to discriminate the two classes.
It appears that the GLM (aggregated AUROC was 0.77) is slightly better than the SVM in this specific case.
To guarantee an absolute fair comparison, one should also make sure that the two models use the exact same partitions – something we have not shown here but have silently used in the background (see code/12_cv.R in the book’s GitHub repository for more information).
To do so, mlr3 offers the functions benchmark_grid() and benchmark() (see also https://mlr3book.mlr-org.com/chapters/chapter3/evaluation_and_benchmarking.html#sec-benchmarking, Becker et al. 2022).
We will explore these functions in more detail in the Exercises.
Please note also that using more than 50 iterations in the random search of the SVM would probably yield hyperparameters that result in models with a better AUROC (Schratz et al. 2019).
On the other hand, increasing the number of random search iterations would also increase the total number of models and thus runtime.
So far spatial CV has been used to assess the ability of learning algorithms to generalize to unseen data. For predictive mapping purposes, one would tune the hyperparameters on the complete dataset. This will be covered in Chapter 15.
12.6 Conclusions
Resampling methods are an important part of a data scientist’s toolbox (James et al. 2013). This chapter used cross-validation to assess predictive performance of various models. As described in Section 12.4, observations with spatial coordinates may not be statistically independent due to spatial autocorrelation, violating a fundamental assumption of cross-validation. Spatial CV addresses this issue by reducing bias introduced by spatial autocorrelation.
The mlr3 package facilitates (spatial) resampling techniques in combination with the most popular statistical learning techniques including linear regression, semi-parametric models such as generalized additive models and machine learning techniques such as random forests, SVMs, and boosted regression trees (Bischl et al. 2016; Schratz et al. 2019). Machine learning algorithms often require hyperparameter inputs, the optimal ‘tuning’ of which can require thousands of model runs which require large computational resources, consuming much time, RAM and/or cores. mlr3 tackles this issue by enabling parallelization.
Machine learning overall, and its use to understand spatial data, is a large field and this chapter has provided the basics, but there is more to learn. We recommend the following resources in this direction:
- The mlr3 book (Becker et al. (2022); https://mlr3book.mlr-org.com/) and especially the chapter on the handling of spatio-temporal data
- An academic paper on hyperparameter tuning (Schratz et al. 2019)
- An academic paper on how to use mlr3spatiotempcv (Schratz et al. 2021)
- In case of spatio-temporal data, one should account for spatial and temporal autocorrelation when doing CV (Meyer et al. 2018)
12.7 Exercises
E1. Compute the following terrain attributes from the elev dataset loaded with terra::rast(system.file("raster/ta.tif", package = "spDataLarge"))$elev with the help of R-GIS bridges (see the bridges to GIS software chapter):
- Slope
- Plan curvature
- Profile curvature
- Catchment area
E2. Extract the values from the corresponding output rasters to the lsl data frame (data("lsl", package = "spDataLarge") by adding new variables called slope, cplan, cprof, elev and log_carea.
E3. Use the derived terrain attribute rasters in combination with a GLM to make a spatial prediction map similar to that shown in Figure 12.2.
Running data("study_mask", package = "spDataLarge") attaches a mask of the study area.
E4. Compute a 100-repeated 5-fold non-spatial cross-validation and spatial CV based on the GLM learner and compare the AUROC values from both resampling strategies with the help of boxplots.
Hint: You need to specify a non-spatial resampling strategy.
Another hint: You might want to solve Excercises 4 to 6 in one go with the help of mlr3::benchmark() and mlr3::benchmark_grid() (for more information, please refer to https://mlr3book.mlr-org.com/chapters/chapter10/advanced_technical_aspects_of_mlr3.html#sec-fallback).
When doing so, keep in mind that the computation can take very long, probably several days.
This, of course, depends on your system.
Computation time will be shorter the more RAM and cores you have at your disposal.
E5. Model landslide susceptibility using a quadratic discriminant analysis (QDA). Assess the predictive performance of the QDA. What is the a difference between the spatially cross-validated mean AUROC value of the QDA and the GLM?
E6. Run the SVM without tuning the hyperparameters.
Use the rbfdot kernel with \(\sigma\) = 1 and C = 1.
Leaving the hyperparameters unspecified in kernlab’s ksvm() would otherwise initialize an automatic non-spatial hyperparameter tuning.