13 Transportation

Prerequisites

• This chapter uses the following packages:⁹⁰

library(sf)
library(dplyr)
library(spDataLarge)
library(stplanr)      # for processing geographic transport data
library(tmap)         # map making (see Chapter 9)
library(ggplot2)      # data visualization package
library(sfnetworks)   # spatial network classes and functions 

13.1 Introduction

In few other sectors is geographic space more tangible than transportation. The effort of moving (overcoming distance) is central to the ‘first law’ of geography, defined by Waldo Tobler in 1970 as follows (Waldo R. Tobler 1970):

Everything is related to everything else, but near things are more related than distant things.

This ‘law’ is the basis for spatial autocorrelation and other key geographic concepts. It applies to phenomena as diverse as friendship networks and ecological diversity and can be explained by the costs of transport — in terms of time, energy and money — which constitute the ‘friction of distance’. From this perspective, transport technologies are disruptive, changing spatial relationships between geographic entities including mobile humans and goods: “the purpose of transportation is to overcome space” (Rodrigue, Comtois, and Slack 2013).

Transport is an inherently spatial activity, involving moving from an origin point ‘A’ to a destination point ‘B’, through infinite localities in between. It is therefore unsurprising that transport researchers have long turned to geographic and computational methods to understand movement patterns, and how interventions can improve their performance (Lovelace 2021).

This chapter introduces the geographic analysis of transport systems at different geographic levels:

• Areal units: transport patterns can be understood with reference to zonal aggregates, such as the main mode of travel (by car, bike or foot, for example), and average distance of trips made by people living in a particular zone, covered in Section 13.3
• Desire lines: straight lines that represent ‘origin-destination’ data that records how many people travel (or could travel) between places (points or zones) in geographic space, the topic of Section 13.4
• Nodes: these are points in the transport system that can represent common origins and destinations and public transport stations such as bus stops and rail stations, the topic of Section 13.5
• Routes: these are lines representing a path along the route network along the desire lines and between nodes. Routes (which can be represented as single linestrings or multiple short segments) and the routing engines that generate them, are covered in Section 13.6
• Route networks: these represent the system of roads, paths and other linear features in an area and are covered in Section 13.7. They can be represented as geographic features (typically short segments of road that add up to create a full network) or structured as an interconnected graph, with the level of traffic on different segments referred to as ‘flow’ by transport modelers (Hollander 2016)

Another key level is agents, mobile entities like you and me and vehicles that enable us to move such as bikes and buses. These can be represented computationally in software such as MATSim and A/B Street, which represent the dynamics of transport systems using an agent-based modeling (ABM) framework, usually at high levels of spatial and temporal resolution (Horni, Nagel, and Axhausen 2016). ABM is a powerful approach to transport research with great potential for integration with R’s spatial classes (Thiele 2014; Lovelace and Dumont 2016), but is outside the scope of this chapter. Beyond geographic levels and agents, the basic unit of analysis in many transport models is the trip, a single purpose journey from an origin ‘A’ to a destination ‘B’ (Hollander 2016). Trips join-up the different levels of transport systems and can be represented simplistically as geographic desire lines connecting zone centroids (nodes) or as routes that follow the transport route network. In this context, agents are usually point entities that move within the transport network.

Transport systems are dynamic (Xie and Levinson 2011). While the focus of this chapter is the geographic analysis of a transport systems, it provides insights into how the approach can be used to simulate scenarios of change, in Section 13.8. The purpose of geographic transport modeling can be interpreted as simplifying the complexity of these spatio-temporal systems in ways that capture their essence. Selecting appropriate levels of geographic analysis can help simplify this complexity without losing its most important features and variables, enabling better decision making and more effective interventions (Hollander 2016).

Typically, models are designed to tackle a particular problem, such as how to improve safety or the environmental performance of transport systems. For this reason, this chapter is based around a policy scenario, introduced in the next section, that asks: how to increase cycling in the city of Bristol? Chapter 14 demonstrates a related application of geocomputation: prioritizing the location of new bike shops. There is a link between the chapters: new and effectively-located cycling infrastructure can get people cycling, boosting demand for bike shops and local economic activity. This highlights an important feature of transport systems: they are closely linked to broader phenomena and land-use patterns.

13.2 A case study of Bristol

The case study used for this chapter is located in Bristol, a city in the west of England, around 30 km east of the Welsh capital Cardiff. An overview of the region’s transport network is illustrated in Figure 13.1, which shows a diversity of transport infrastructure, for cycling, public transport, and private motor vehicles.

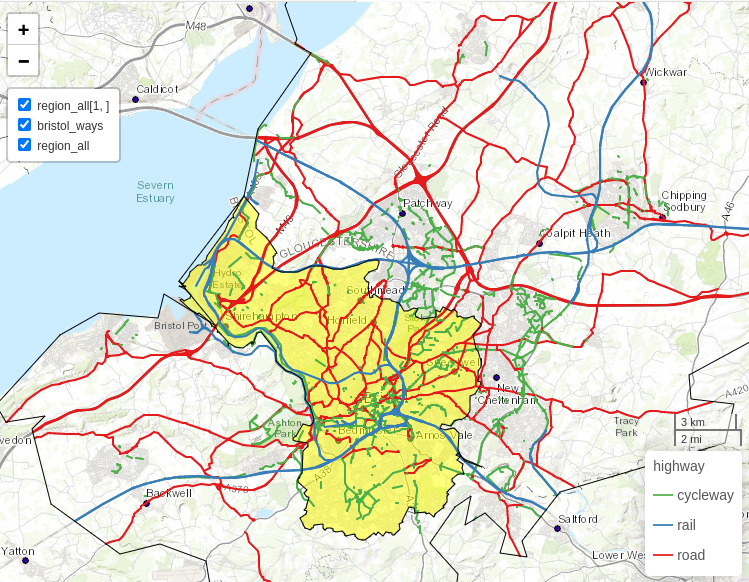
FIGURE 13.1: Bristol’s transport network represented by colored lines for active (green), public (railways, blue) and private motor (red) modes of travel. Black border lines represent the inner city boundary (highlighted in yellow) and the larger Travel To Work Area (TTWA).

Bristol is the 10^th largest city council in England, with a population of half a million people, although its travel catchment area is larger (see Section 13.3). It has a vibrant economy with aerospace, media, financial service and tourism companies, alongside two major universities. Bristol shows a high average income per person but also contains areas of severe deprivation (Bristol City Council 2015).

In terms of transport, Bristol is well served by rail and road links, and has a relatively high level of active travel. 19% of its citizens cycle and 88% walk at least once per month according to the Active People Survey (the national average is 15% and 81%, respectively). 8% of the population said they cycled to work in the 2011 census, compared with only 3% nationwide.

Like many cities, Bristol has major congestion, air quality and physical inactivity problems. Cycling can tackle all of these issues efficiently: it has a greater potential to replace car trips than walking, with typical speeds of 15-20 km/h vs 4-6 km/h for walking. For this reason Bristol’s Transport Strategy has ambitious plans for cycling.

To highlight the importance of policy considerations in transportation research, this chapter is guided by the need to provide evidence for people (transport planners, politicians and other stakeholders) tasked with getting people out of cars and onto more sustainable modes — walking and cycling in particular. The broader aim is to demonstrate how geocomputation can support evidence-based transport planning. In this chapter you will learn how to:

• Describe the geographical patterns of transport behavior in cities
• Identify key public transport nodes supporting multi-modal trips
• Analyze travel ‘desire lines’ to find where many people drive short distances
• Identify cycle route locations that will encourage less car driving and more cycling

To get the wheels rolling on the practical aspects of this chapter, the next section begins by loading zonal data on travel patterns. These zone-level datasets are small but often vital for gaining a basic understanding of a settlement’s overall transport system.

13.3 Transport zones

Although transport systems are primarily based on linear features and nodes — including pathways and stations — it often makes sense to start with areal data, to break continuous space into tangible units (Hollander 2016). In addition to the boundary defining the study area (Bristol in this case), two zone types are of particular interest to transport researchers: origin and destination zones. Often, the same geographic units are used for origins and destinations. However, different zoning systems, such as ‘Workplace Zones’, may be appropriate to represent the increased density of trip destinations in areas with many ‘trip attractors’ such as schools and shops (Office for National Statistics 2014).

The simplest way to define a study area is often the first matching boundary returned by OpenStreetMap. This can be done with a command such as osmdata::getbb("Bristol", format_out = "sf_polygon", limit = 1). This returns an sf object (or a list of sf objects if limit = 1 is not specified) representing the bounds of the largest matching city region, either a rectangular polygon of the bounding box or a detailed polygonal boundary.⁹¹ For Bristol, a detailed polygon is returned, as represented by the bristol_region object in the spDataLarge package. See the inner blue boundary in Figure 13.1: there are a couple of issues with this approach:

• The first boundary returned by OSM may not be the official boundary used by local authorities
• Even if OSM returns the official boundary, this may be inappropriate for transport research because they bear little relation to where people travel

Travel to Work Areas (TTWAs) address these issues by creating a zoning system analogous to hydrological watersheds. TTWAs were first defined as contiguous zones within which 75% of the population travels to work (Coombes, Green, and Openshaw 1986), and this is the definition used in this chapter. Because Bristol is a major employer attracting travel from surrounding towns, its TTWA is substantially larger than the city bounds (see Figure 13.1). The polygon representing this transport-orientated boundary is stored in the object bristol_ttwa, provided by the spDataLarge package loaded at the beginning of this chapter.

The origin and destination zones used in this chapter are the same: officially defined zones of intermediate geographic resolution (their official name is Middle layer Super Output Areas or MSOAs). Each houses around 8,000 people. Such administrative zones can provide vital context to transport analysis, such as the type of people who might benefit most from particular interventions (e.g., Moreno-Monroy, Lovelace, and Ramos (2017)).

The geographic resolution of these zones is important: small zones with high geographic resolution are usually preferable but their high number in large regions can have consequences for processing (especially for origin-destination analysis in which the number of possibilities increases as a non-linear function of the number of zones) (Hollander 2016).

Another issue with small zones is related to anonymity rules. To make it impossible to infer the identity of individuals in zones, detailed socio-demographic variables are often only available at a low geographic resolution. Breakdowns of travel mode by age and sex, for example, are available at the Local Authority level in the UK, but not at the much higher Output Area level, each of which contains around 100 households. For further details, see www.ons.gov.uk/methodology/geography.

The 102 zones used in this chapter are stored in bristol_zones, as illustrated in Figure 13.2. Note the zones get smaller in densely populated areas: each houses a similar number of people. bristol_zones contains no attribute data on transport, however, only the name and code of each zone:

names(bristol_zones)
#> [1] "geo_code" "name"     "geometry"

To add travel data, we will perform an attribute join, a common task described in Section 3.2.4. We will use travel data from the UK’s 2011 census question on travel to work, data stored in bristol_od, which was provided by the ons.gov.uk data portal. bristol_od is an origin-destination (OD) dataset on travel to work between zones from the UK’s 2011 Census (see Section 13.4). The first column is the ID of the zone of origin and the second column is the zone of destination. bristol_od has more rows than bristol_zones, representing travel between zones rather than the zones themselves:

nrow(bristol_od)
#> [1] 2910
nrow(bristol_zones)
#> [1] 102

The results of the previous code chunk shows that there are more than 10 OD pairs for every zone, meaning we will need to aggregate the origin-destination data before it is joined with bristol_zones, as illustrated below (origin-destination data is described in Section 13.4).

zones_attr = bristol_od |> 
  group_by(o) |> 
  summarize(across(where(is.numeric), sum)) |> 
  dplyr::rename(geo_code = o)

The preceding chunk:

• Grouped the data by zone of origin (contained in the column o)
• Aggregated the variables in the bristol_od dataset if they were numeric, to find the total number of people living in each zone by mode of transport⁹²
• Renamed the grouping variable o so it matches the ID column geo_code in the bristol_zones object

The resulting object zones_attr is a data frame with rows representing zones and an ID variable. We can verify that the IDs match those in the zones dataset using the %in% operator as follows:

summary(zones_attr$geo_code %in% bristol_zones$geo_code)
#>    Mode    TRUE 
#> logical     102

The results show that all 102 zones are present in the new object and that zone_attr is in a form that can be joined onto the zones.⁹³ This is done using the joining function left_join() (note that inner_join() would produce here the same result):

zones_joined = left_join(bristol_zones, zones_attr, by = "geo_code")
sum(zones_joined$all)
#> [1] 238805
names(zones_joined)
#> [1] "geo_code"   "name"       "all"        "bicycle"    "foot"      
#> [6] "car_driver" "train"      "geometry"

The result is zones_joined, which contains new columns representing the total number of trips originating in each zone in the study area (almost 1/4 of a million) and their mode of travel (by bicycle, foot, car and train). The geographic distribution of trip origins is illustrated in the left-hand map in Figure 13.2. This shows that most zones have between 0 and 4,000 trips originating from them in the study area. More trips are made by people living near the center of Bristol and fewer on the outskirts. Why is this? Remember that we are only dealing with trips within the study region: low trip numbers in the outskirts of the region can be explained by the fact that many people in these peripheral zones will travel to other regions outside of the study area. Trips outside the study region can be included in regional model by a special destination ID covering any trips that go to a zone not represented in the model (Hollander 2016). The data in bristol_od, however, simply ignores such trips: it is an ‘intra-zonal’ model.

In the same way that OD datasets can be aggregated to the zone of origin, they can also be aggregated to provide information about destination zones. People tend to gravitate towards central places. This explains why the spatial distribution represented in the right panel in Figure 13.2 is relatively uneven, with the most common destination zones concentrated in Bristol city center. The result is zones_od, which contains a new column reporting the number of trip destinations by any mode, is created as follows:

zones_destinations = bristol_od |> 
  group_by(d) |> 
  summarize(across(where(is.numeric), sum)) |> 
  select(geo_code = d, all_dest = all)
zones_od = inner_join(zones_joined, zones_destinations, by = "geo_code")

A simplified version of Figure 13.2 is created with the code below (see 13-zones.R in the code folder of the book’s GitHub repository to reproduce the figure and Section 9.2.7 for details on faceted maps with tmap):

qtm(zones_od, c("all", "all_dest")) +
  tm_layout(panel.labels = c("Origin", "Destination"))

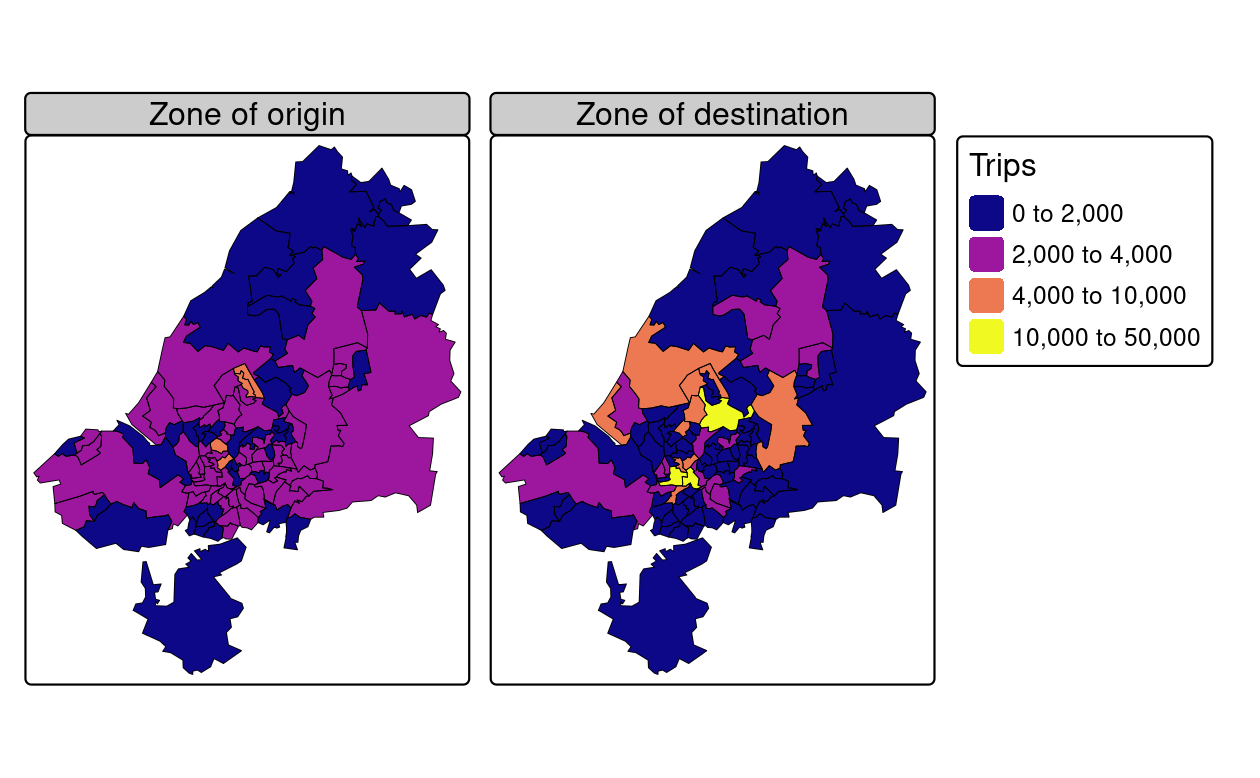
FIGURE 13.2: Number of trips (commuters) living and working in the region. The left map shows zone of origin of commute trips; the right map shows zone of destination (generated by the script 13-zones.R).

13.4 Desire lines

Desire lines connect origins and destinations, representing where people desire to go, typically between zones. They represent the quickest ‘bee line’ or ‘crow flies’ route between A and B that would be taken, if it were not for obstacles such as buildings and windy roads getting in the way (we will see how to convert desire lines into routes in the next section). Typically, desire lines are represented geographically as starting and ending in the geographic (or population weighted) centroid of each zone. This is the type of desire line that we will create and use in this section, although it is worth being aware of ‘jittering’ techniques that enable multiple start and end points to increase the spatial coverage and accuracy of analyses building on OD data (Lovelace, Félix, and Carlino 2022).

We have already loaded data representing desire lines in the dataset bristol_od. This origin-destination (OD) data frame object represents the number of people traveling between the zone represented in o and d, as illustrated in Table 13.1. To arrange the OD data by all trips and then filter-out only the top 5, type (please refer to Chapter 3 for a detailed description of non-spatial attribute operations):

od_top5 = bristol_od |> 
  slice_max(all, n = 5)

TABLE 13.1: Sample of the top 5 origin-destination pairs in the Bristol OD data frame, representing travel desire lines between zones in the study area.

o	d	all	bicycle	foot	car_driver	train
E02003043	E02003043	1493	66	1296	64	8
E02003047	E02003043	1300	287	751	148	8
E02003031	E02003043	1221	305	600	176	7
E02003037	E02003043	1186	88	908	110	3
E02003034	E02003043	1177	281	711	100	7

The resulting table provides a snapshot of Bristolian travel patterns in terms of commuting (travel to work). It demonstrates that walking is the most popular mode of transport among the top 5 origin-destination pairs, that zone E02003043 is a popular destination (Bristol city center, the destination of all the top 5 OD pairs), and that the intrazonal trips, from one part of zone E02003043 to another (first row of Table 13.1), constitute the most traveled OD pair in the dataset. But from a policy perspective, the raw data presented in Table 13.1 is of limited use: aside from the fact that it contains only a tiny portion of the 2,910 OD pairs, it tells us little about where policy measures are needed, or what proportion of trips are made by walking and cycling. The following command calculates the percentage of each desire line that is made by these active modes:

bristol_od$Active = (bristol_od$bicycle + bristol_od$foot) /
  bristol_od$all * 100

There are two main types of OD pairs: interzonal and intrazonal. Interzonal OD pairs represent travel between zones in which the destination is different from the origin. Intrazonal OD pairs represent travel within the same zone (see the top row of Table 13.1). The following code chunk splits od_bristol into these two types:

od_intra = filter(bristol_od, o == d)
od_inter = filter(bristol_od, o != d)

The next step is to convert the interzonal OD pairs into an sf object representing desire lines that can be plotted on a map with the stplanr function od2line().⁹⁴

desire_lines = od2line(od_inter, zones_od)
#> Creating centroids representing desire line start and end points.

An illustration of the results is presented in Figure 13.3, a simplified version of which is created with the following command (see the code in 13-desire.R to reproduce the figure exactly and Chapter 9 for details on visualization with tmap):

qtm(desire_lines, lines.lwd = "all")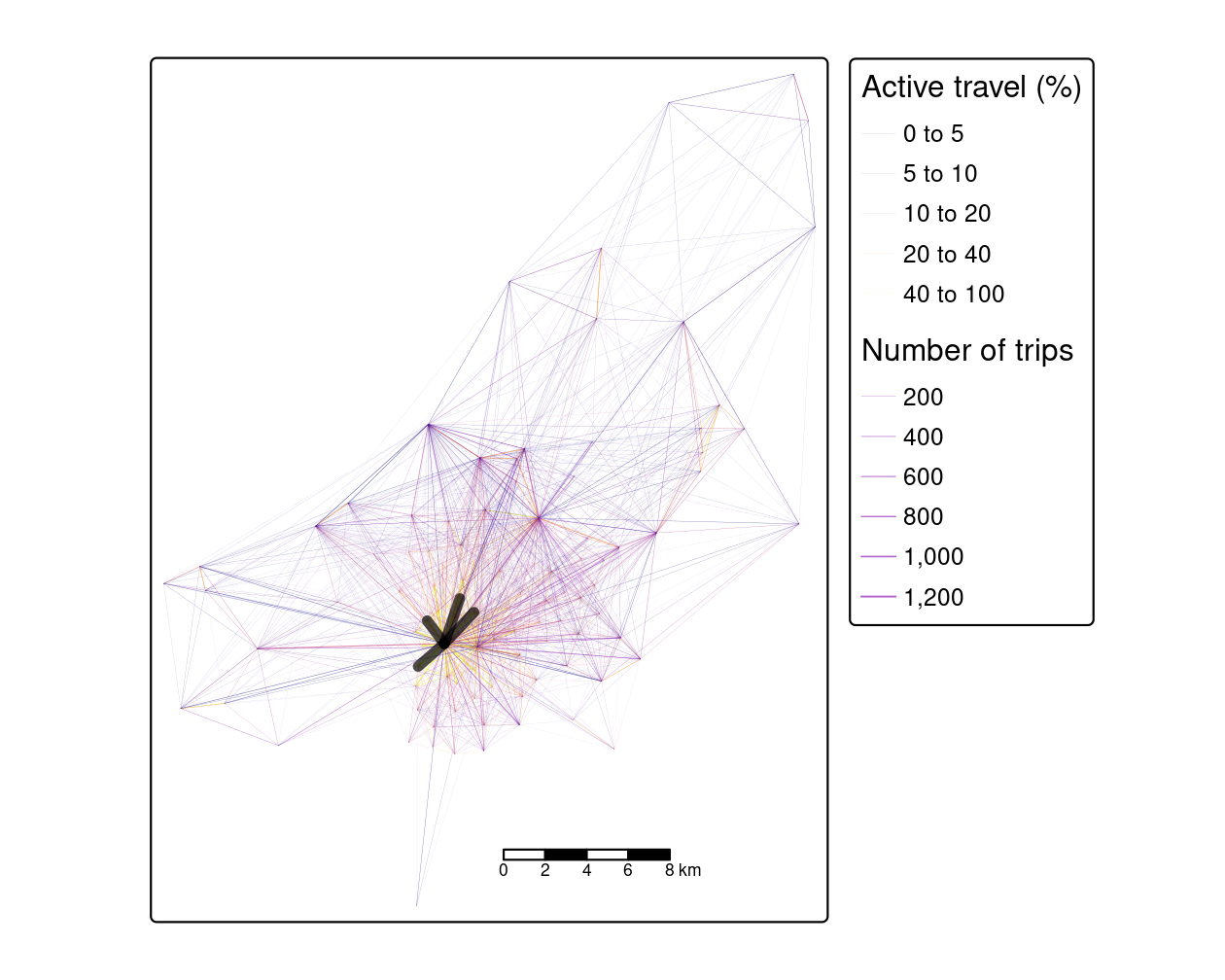

FIGURE 13.3: Desire lines representing trip patterns in Bristol, with width representing number of trips and color representing the percentage of trips made by active modes (walking and cycling). The four black lines represent the interzonal OD pairs in Table 13.1.

The map shows that the city center dominates transport patterns in the region, suggesting policies should be prioritized there, although a number of peripheral sub-centers can also be seen. Desire lines are important generalized components of transport systems. More concrete components include nodes, which have specific destinations (rather than hypothetical straight lines represented in desire lines). Nodes are covered in the next section.

13.5 Nodes

Nodes in geographic transport datasets are points among the predominantly linear features that comprise transport networks. Broadly are two main types of transport nodes:

1. Nodes not directly on the network such as zone centroids or individual origins and destinations such as houses and workplaces
2. Nodes that are a part of transport networks. Technically, a node can be located at any point on a transport network but in practice they are often special kinds of vertex such as intersections between pathways (junctions) and points for entering or exiting a transport network such as bus stops and train stations⁹⁵

Transport networks can be represented as graphs, in which each segment is connected (via edges representing geographic lines) to one or more other edges in the network. Nodes outside the network can be added with “centroid connectors”, new route segments to nearby nodes on the network (Hollander 2016).⁹⁶ Every node in the network is then connected by one or more ‘edges’ that represent individual segments on the network. We will see how transport networks can be represented as graphs in Section 13.7.

Public transport stops are particularly important nodes that can be represented as either type of node: a bus stop that is part of a road, or a large rail station that is represented by its pedestrian entry point hundreds of meters from railway tracks. We will use railway stations to illustrate public transport nodes, in relation to the research question of increasing cycling in Bristol. These stations are provided by spDataLarge in bristol_stations.

A common barrier preventing people from switching away from cars for commuting to work is that the distance from home to work is too far to walk or cycle. Public transport can reduce this barrier by providing a fast and high-volume option for common routes into cities. From an active travel perspective, public transport ‘legs’ of longer journeys divide trips into three:

• The origin leg, typically from residential areas to public transport stations
• The public transport leg, which typically goes from the station nearest a trip’s origin to the station nearest its destination
• The destination leg, from the station of alighting to the destination

Building on the analysis conducted in Section 13.4, public transport nodes can be used to construct three-part desire lines for trips that can be taken by bus and (the mode used in this example) rail. The first stage is to identify the desire lines with most public transport travel, which in our case is easy because our previously created dataset desire_lines already contains a variable describing the number of trips by train (the public transport potential could also be estimated using public transport routing services such as OpenTripPlanner). To make the approach easier to follow, we will select only the top three desire lines in terms of rails use:

desire_rail = top_n(desire_lines, n = 3, wt = train)

The challenge now is to ‘break-up’ each of these lines into three pieces, representing travel via public transport nodes. This can be done by converting a desire line into a multilinestring object consisting of three line geometries representing origin, public transport and destination legs of the trip. This operation can be divided into three stages: matrix creation (of origins, destinations and the ‘via’ points representing rail stations), identification of nearest neighbors and conversion to multilinestrings. These are undertaken by line_via(). This stplanr function takes input lines and points and returns a copy of the desire lines — see the ?line_via() for details on how this works. The output is the same as the input line, except it has new geometry columns representing the journey via public transport nodes, as demonstrated below:

ncol(desire_rail)
#> [1] 9
desire_rail = line_via(desire_rail, bristol_stations)
ncol(desire_rail)
#> [1] 12

As illustrated in Figure 13.4, the initial desire_rail lines now have three additional geometry list columns representing travel from home to the origin station, from there to the destination, and finally from the destination station to the destination. In this case, the destination leg is very short (walking distance) but the origin legs may be sufficiently far to justify investment in cycling infrastructure to encourage people to cycle to the stations on the outward leg of peoples’ journey to work in the residential areas surrounding the three origin stations in Figure 13.4.

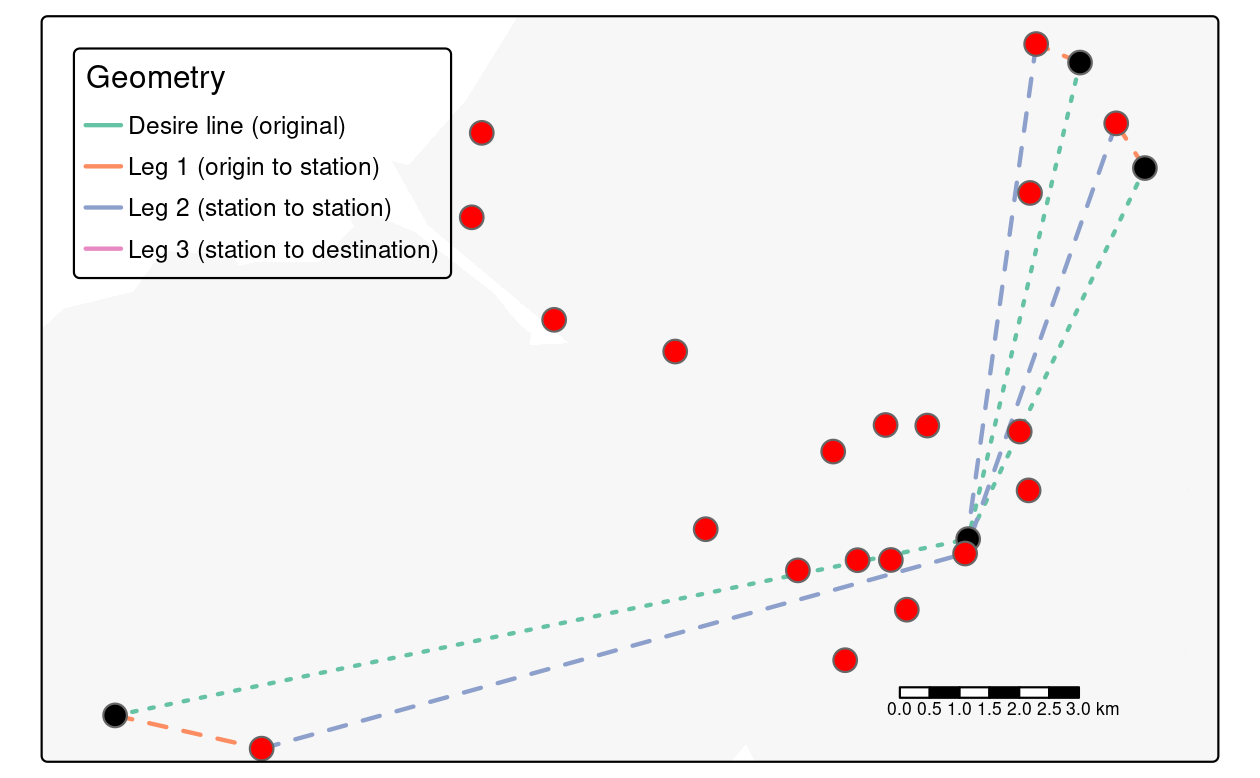
FIGURE 13.4: Station nodes (red dots) used as intermediary points that convert straight desire lines with high rail usage (thin green lines) into three legs: to the origin station (orange) via public transport (blue) and to the destination (pink, not visible because it is so short).

13.6 Routes

From a geographical perspective, routes are desire lines that are no longer straight: the origin and destination points are the same as in the desire line representation of travel, but the pathway to get from A to B is more complex. The geometries of routes are typically (but not always) determined by the transport network.

While desire lines contain only two vertices (their beginning and end points), routes can contain any number of vertices, representing points between A and B joined by straight lines: the definition of a linestring geometry. Routes covering large distances or following intricate network can have many hundreds of vertices; routes on grid-based or simplified road networks tend to have fewer.

Routes are generated from desire lines or, more commonly, matrices containing coordinate pairs representing desire lines. This routing process is done by a range of broadly-defined routing engines: software and web services that return geometries and attributes describing how to get from origins to destinations. Routing engines can be classified based on where they run relative to R:

• In-memory routing using R packages that enable route calculation (described in Section 13.6.2)
• Locally hosted routing engines external to R that can be called from R (Section 13.6.3)
• Remotely hosted routing engines by external entities that provide a web API that can be called from R (Section 13.6.4)

Before describing each, it is worth outlining other ways of categorizing routing engines. Routing engines can be multi-modal, meaning that they can calculate trips composed of more than one mode of transport, or not. Multi-modal routing engines can return results consisting of multiple legs, each one made by a different mode of transport. The optimal route from a residential area to a commercial area could involve 1) walking to the nearest bus stop, 2) catching the bus to the nearest node to the destination, and 3) walking to the destination, given a set of input parameters. The transition points between these three legs are commonly referred to as ‘ingress’ and ‘egress’, meaning getting on/off a public transport vehicle. Multi-modal routing engines such as R5 are more sophisticated and have larger input data requirements than ‘uni-modal’ routing engines such as OSRM (described in Section 13.6.3).

A major strength of multi-modal engines is their ability to represent ‘transit’ (public transport) trips by trains, buses etc. Multi-model routing engines require input datasets representing public transport networks, typically in General Transit Feed Specification (GTFS) files, which can be processed with functions in the tidytransit and gtfstools packages (other packages and tools for working with GTFS files are available). Single mode routing engines may be sufficient for projects focused on specific (non public) modes of transport. Another way of classifying routing engines (or settings) is by the geographic level of the outputs: routes, legs and segments.

13.6.1 Routes, legs and segments

Routing engines can generate outputs at three geographic levels of routes, legs and segments:

• Route level outputs contain a single feature (typically a multilinestring and associated row in the data frame representation) per origin-destination pair, meaning a single row of data per trip
• Leg level outputs contain a single feature and associated attributes each mode within each origin-destination pair, as described in Section 13.5. For trips only involving one mode (for example driving from home to work, ignoring the short walk to the car) the leg is the same as the route: the car journey. For trips involving public transport, legs provide key information. The r5r function detailed_itineraries() returns legs which, confusingly, are sometimes referred to as ‘segments’
• Segment level outputs provide the most detailed information about routes, with records for each small section of the transport network. Typically segments are similar in length, or identical to, ways in OpenStreetMap. The cyclestreets function journey() returns data at the segment level which can be aggregated by grouping by origin and destination level data returned by the route() function in stplanr

Most routing engines return route level by default, although multi-modal engines generally provide outputs at the leg level (one feature per continuous movement by a single mode of transport). Segment level outputs have the advantage of providing more detail. The cyclestreets package returns multiple ‘quietness’ levels per route, enabling identification of the ‘weakest link’ in cycle networks. Disadvantages of segment level outputs include increased file sizes and complexities associated with the extra detail.

Route level results can be converted into segment level results using the function stplanr::overline() (Morgan and Lovelace 2020). When working with segment or leg-level data, route-level statistics can be returned by grouping by columns representing trip start and end points and summarizing/aggregating columns containing segment-level data.

13.6.2 In-memory routing with R

Routing engines in R enable route networks stored as R objects in memory to be used as the basis of route calculation. Options include sfnetworks, dodgr and cppRouting packages, each of which provide their own class system to represent route networks, the topic of the next section.

While fast and flexible, native R routing options are generally harder to set-up than dedicated routing engines for realistic route calculation. Routing is a hard problem and many hundreds of hours have been put into open source routing engines that can be downloaded and hosted locally. On the other hand, R-based routing engines may be well-suited to model experiments and the statistical analysis of the impacts of changes on the network. Changing route network characteristics (or weights associated with different route segment types), re-calculating routes, and analyzing results under many scenarios in a single language has benefits for research applications.

13.6.3 Locally hosted dedicated routing engines

Locally hosted routing engines include OpenTripPlanner, Valhalla, and R5 (which are multi-modal), and the OpenStreetMap Routing Machine (OSRM) (which is ‘uni-modal’). These can be accessed from R with the packages opentripplanner, valhallr, r5r and osrm (Morgan et al. 2019; Pereira et al. 2021). Locally hosted routing engines run on the user’s computer but in a process separate from R. They benefit from speed of execution and control over the weighting profile for different modes of transport. Disadvantages include the difficulty of representing complex networks locally; temporal dynamics (primarily due to traffic); and the need for specialized external software.

13.6.4 Remotely hosted dedicated routing engines

Remotely hosted routing engines use a web API to send queries about origins and destinations and return results. Routing services based on open source routing engines, such as OSRM’s publicly available service, work the same when called from R as locally hosted instances, simply requiring arguments specifying ‘base URLs’ to be updated. However, the fact that external routing services are hosted on a dedicated machine (usually funded by commercial company with incentives to generate accurate routes) can give them advantages, including:

• Provision of routing services worldwide (or usually at least over a large region)
• Established routing services are usually updated regularly and can often respond to traffic levels
• Routing services usually run on dedicated hardware and software including systems such as load balancers to ensure consistent performance

Disadvantages of remote routing services include speed when batch jobs are not possible (they often rely on data transfer over the internet on a route-by-route basis), price (the Google routing API, for example, limits the number of free queries) and licensing issues. googleway and mapbox packages demonstrate this approach by providing access to routing services from Google and Mapbox, respectively. Free (but rate limited) routing service include OSRM and openrouteservice.org which can be accessed from R with the osrm and openrouteservice packages, the latter of which is not on CRAN. There are also more specific routing services such as that provided by CycleStreets.net, a cycle journey planner and not-for-profit transport technology company “for cyclists, by cyclists”. While R users can access CycleStreets routes via the package cyclestreets, many routing services lack R interfaces, representing a substantial opportunity for package development: building an R package to provide an interface to a web API can be a rewarding experience.

13.6.5 Contraction hierarchies and traffic assigment

Contraction hierarchies and traffic assignment are advanced but important topics in transport modeling worth being aware of, especially if you want your code to scale to large networks. Calculating many routes is computationally resource intensive and can take hours, leading to the development of several algorithms to speed-up routing calculations. Contraction hierarchies is a well-known algorithm that can lead to a substantial (1000x+ in some cases) speed-up in routing tasks, depending on network size. Contraction hierarchies are used behind the scenes in the routing engines mentioned in the previous sections.

Traffic assignment is a problem that is closely related to routing: in practice, the shortest path between two points is not always the fastest, especially if there is congestion. The process takes OD datasets, of the kind described in Section 13.4, and assigns traffic to each segment in the network, generating route networks of the kind described in Section 13.7. An established solution is Wardrop’s principle of user equilibrium which shows that, to be realistic, congestion should be considered when estimating flows on the network, with reference to a mathematically defined relationship between cost and flow (Wardrop 1952). This optimization problem can be solved by iterative algorithms which are implemented in the cppRouting package, which also implements contraction hierarchies for fast routing.

13.6.6 Routing: A worked example

Instead of routing all desire lines generated in Section 13.4, we focus on a subset that is highly policy relevant. Running a computationally intensive operation on a subset before trying to process the whole dataset is often sensible, and this applies to routing. Routing can be time and memory-consuming, resulting in large objects, due to the detailed geometries and extra attributes of route objects. We will therefore filter the desire lines before calculating routes in this section.

Cycling is most beneficial when it replaces car trips. Short trips (around 5 km, which can be cycled in 15 minutes at a speed of 20 km/hr) have a relatively high probability of being cycled, and the maximum distance increases when trips are made by electric bike (Lovelace et al. 2017). These considerations inform the following code chunk which filters the desire lines and returns the object desire_lines_short representing OD pairs between which many (100+) short (2.5 to 5 km Euclidean distance) trips are driven:

desire_lines$distance_km = as.numeric(st_length(desire_lines)) / 1000
desire_lines_short = desire_lines |> 
  filter(car_driver >= 100, distance_km <= 5, distance_km >= 2.5)

In the code above st_length() calculated the length of each desire line, as described in Section 4.2.3. The filter() function from dplyr filtered the desire_lines dataset based on the criteria outlined above, as described in Section 3.2.1. The next stage is to convert these desire lines into routes. This is done using the publicly available OSRM service with the stplanr functions route() and route_osrm() in the code chunk below:

routes_short = route(l = desire_lines_short, route_fun = route_osrm,
                     osrm.profile = "bike")

The output is routes_short, an sf object representing routes on the transport network that are suitable for cycling (according to the OSRM routing engine at least), one for each desire line. Note: calls to external routing engines such as in the command above only work with an internet connection (and sometimes an API key stored in an environment variable, although not in this case). In addition to the columns contained in the desire_lines object, the new route dataset contains distance (referring to route distance this time) and duration columns (in seconds), which provide potentially useful extra information on the nature of each route. We will plot desire lines along which many short car journeys take place alongside cycling routes. Making the width of the routes proportional to the number of car journeys that could potentially be replaced provides an effective way to prioritize interventions on the road network (Lovelace et al. 2017). Figure 13.5 shows routes along which people drive short distances (see the github.com/geocompx for the source code).⁹⁷

FIGURE 13.5: Routes along which many (100+) short (<5km Euclidean distance) car journeys are made (red) overlaying desire lines representing the same trips (black) and zone centroids (dots).

Visualizing the results in an interactive map shows that many short car trips take place in and around Bradley Stoke, around 10 km North of central Bristol. It is easy to find explanations for the area’s high level of car dependency: according to Wikipedia, Bradley Stoke is “Europe’s largest new town built with private investment”, suggesting limited public transport provision. Furthermore, the town is surrounded by large (cycling unfriendly) road structures, including the M4 and M5 motorways (Tallon 2007).

There are many benefits of converting travel desire lines into routes. It is important to remember that we cannot be sure how many (if any) trips will follow the exact routes calculated by routing engines. However, route and street/way/segment level results can be highly policy relevant. Route segment results can enable the prioritization of investment where it is most needed, according to available data (Lovelace et al. 2017).

13.7 Route networks

While routes generally contain data on travel behavior, at the same geographic level as desire lines and OD pairs, route network datasets usually represent the physical transport network. Each segment in a route network roughly corresponds to a continuous section of street between junctions and appears only once, although the average length of segments depends on the data source (segments in the OSM-derived bristol_ways dataset used in this section have an average length of just over 200 m, with a standard deviation of nearly 500 m). Variability in segment lengths can be explained by the fact that in some rural locations junctions are far apart while in dense urban areas there are crossings and other segment breaks every few meters.

Route networks can be an input into, or an output of, transport data analysis projects, or both. Any transport research that involves route calculation requires a route network dataset in the internal or external routing engines (in the latter case the route network data is not necessarily imported into R). However, route networks are also important outputs in many transport research projects: summarizing data such as the potential number of trips made on particular segments and represented as a route network, can help prioritize investment where it is most needed.

To demonstrate how to create route networks as an output derived from route level data, imagine a simple scenario of mode shift. Imagine that 50% of car trips between 0 to 3 km in route distance are replaced by cycling, a percentage that drops by 10 percentage points for every additional km of route distance so that 20% of car trips of 6 km are replaced by cycling and no car trips that are 8 km or longer are replaced by cycling. This is of course an unrealistic scenario (Lovelace et al. 2017), but is a useful starting point. In this case, we can model mode shift from cars to bikes as follows:

uptake = function(x) {
  case_when(
    x <= 3 ~ 0.5,
    x >= 8 ~ 0,
    TRUE ~ (8 - x) / (8 - 3) * 0.5
  )
}
routes_short_scenario = routes_short |> 
  mutate(uptake = uptake(distance / 1000)) |> 
  mutate(bicycle = bicycle + car_driver * uptake,
         car_driver = car_driver * (1 - uptake))
sum(routes_short_scenario$bicycle) - sum(routes_short$bicycle)
#> [1] 3828

Having created a scenario in which approximately 4000 trips have switched from driving to cycling, we can now model where this updated modeled cycling activity will take place. For this, we will use the function overline() from the stplanr package. The function breaks linestrings at junctions (were two or more linestring geometries meet), and calculates aggregate statistics for each unique route segment (Morgan and Lovelace 2020), taking an object containing routes and the names of the attributes to summarize as the first and second argument:

route_network_scenario = overline(routes_short_scenario, attrib = "bicycle")

The outputs of the two preceding code chunks are summarized in Figure 13.6 below.

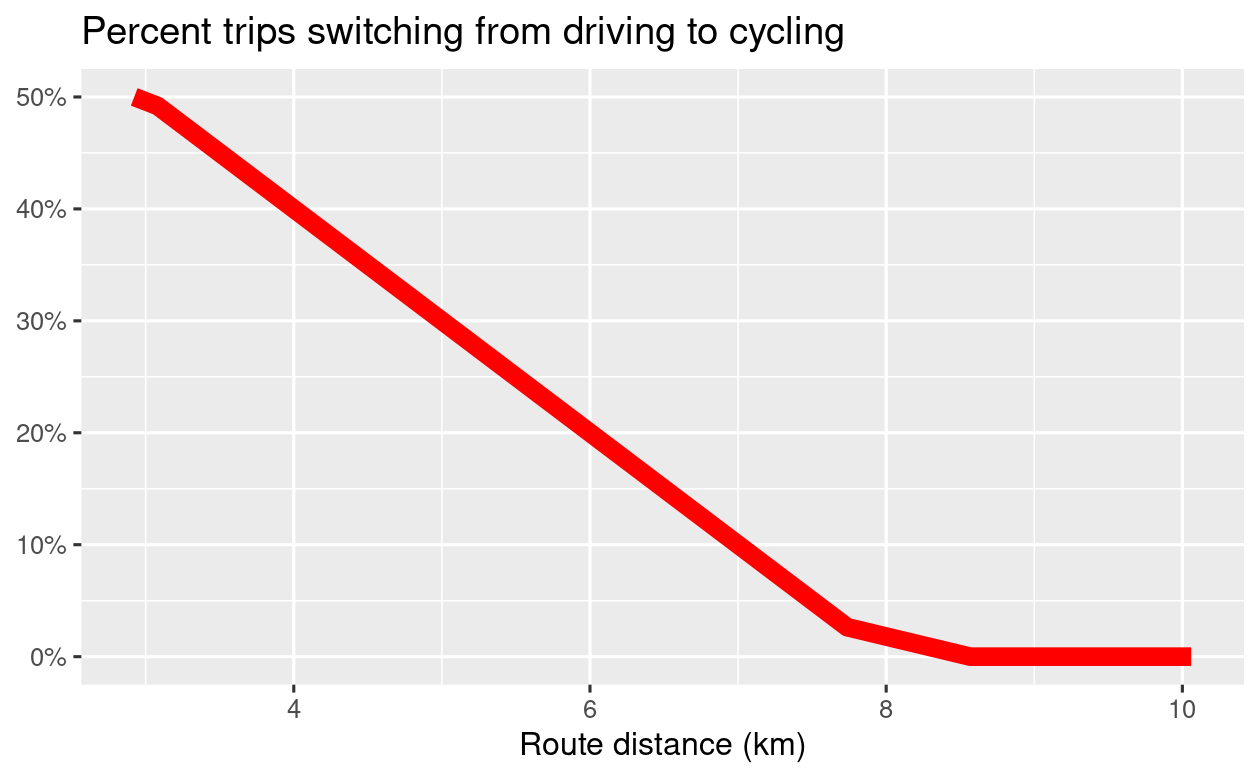
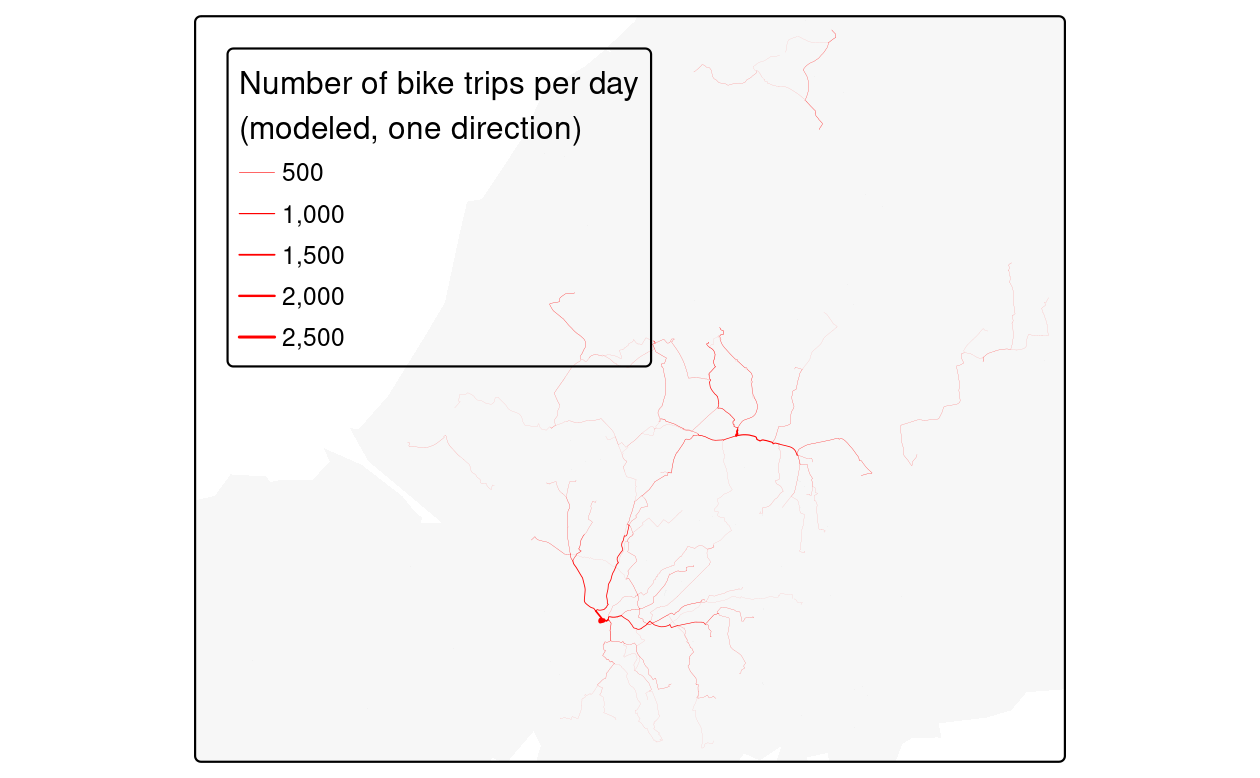
FIGURE 13.6: Illustration of the percentage of car trips switching to cycling as a function of distance (left) and route network level results of this function (right).

Transport networks with records at the segment level, typically with attributes such as road type and width, constitute a common type of route network. Such route network datasets are available worldwide from OpenStreetMap, and can be downloaded with packages such as osmdata and osmextract. To save time downloading and preparing OSM, we will use the bristol_ways object from the spDataLarge package, an sf object with LINESTRING geometries and attributes representing a sample of the transport network in the case study region (see ?bristol_ways for details), as shown in the output below:

summary(bristol_ways)
#>      highway       maxspeed             ref                     geometry   
#>  cycleway:1721   Length:6160        Length:6160        LINESTRING   :6160  
#>  rail    :1017   Class :character   Class :character   epsg:4326    :   0  
#>  road    :3422   Mode  :character   Mode  :character   +proj=long...:   0

The output shows that bristol_ways represents just over 6 thousand segments on the transport network. This and other geographic networks can be represented as mathematical graphs, with nodes on the network, connected by edges. A number of R packages have been developed for dealing with such graphs, notably igraph. You can manually convert a route network into an igraph object, but the geographic attributes will be lost. To overcome this limitation of igraph, the sfnetworks package (van der Meer et al. 2023), which to represent route networks simultaneously as graphs and geographic lines, was developed. We will demonstrate sfnetworks functionality on the bristol_ways object.

bristol_ways$lengths = st_length(bristol_ways)
ways_sfn = as_sfnetwork(bristol_ways)
class(ways_sfn)
#> [1] "sfnetwork" "tbl_graph" "igraph"

ways_sfn
#> # A sfnetwork with 5728 nodes and 4915 edges
#> # A directed multigraph with 1013 components with spatially explicit edges
#> # Node Data:     5,728 × 1 (active)
#> # Edge Data:     4,915 × 7
#>    from    to highway maxspeed ref                              geometry lengths
#>   <int> <int> <fct>   <fct>    <fct>                    <LINESTRING [°]>     [m]
#> 1     1     2 road    <NA>     B3130 (-2.61 51.4, -2.61 51.4, -2.61 51.…    218.
#> # … 

The output of the previous code chunk (with the final output shortened to contain only the most important 8 lines due to space considerations) shows that ways_sfn is a composite object, containing both nodes and edges in graph and spatial form. ways_sfn is of class sfnetwork, which builds on the igraph class from the igraph package. In the example below, the ‘edge betweenness’, meaning the number of shortest paths passing through each edge, is calculated (see ?igraph::betweenness for further details). The output of the edge betweenness calculation is shown Figure 13.7, which has the cycle route network dataset calculated with the overline() function as an overlay for comparison. The results demonstrate that each graph edge represents a segment: the segments near the center of the road network have the highest betweenness values, whereas segments closer to central Bristol have higher cycling potential, based on these simplistic datasets.

ways_centrality = ways_sfn |> 
  activate("edges") |>  
  mutate(betweenness = tidygraph::centrality_edge_betweenness(lengths))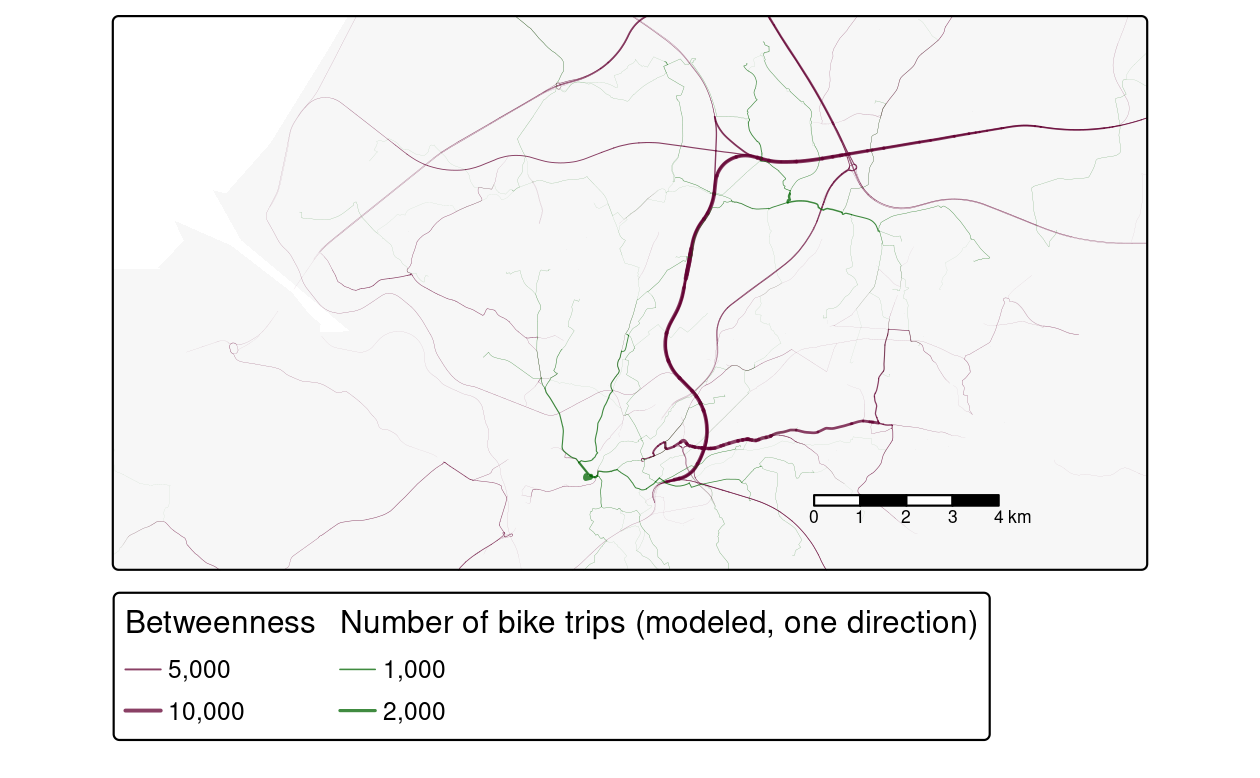 

FIGURE 13.7: Illustration of route network datasets. The grey lines represent a simplified road network, with segment thickness proportional to betweenness. The green lines represent potential cycling flows (one way) calculated with the code above.

One can also find the shortest route between origins and destinations using this graph representation of the route network with the sfnetworks package. The methods presented in this section are relatively simple compared with what is possible. The dual graph/spatial capabilities that sfnetworks enable many new powerful techniques can cannot be fully covered in this section. This section does, however, provide a strong starting point for further exploration and research into the area. A final point is that the example dataset we used above is relatively small. It may also be worth considering how the work could adapt to larger networks: testing methods on a subset of the data, and ensuring you have enough RAM will help, although it’s also worth exploring other tools that can do transport network analysis that are optimized for large networks, such as R5 (Alessandretti et al. 2022).

13.8 Prioritizing new infrastructure

This section demonstrates how geocomputation can create policy relevant outcomes in the field of transport planning. We will identify promising locations for investment in sustainable transport infrastructure, using a simple approach for educational purposes.

An advantage of the data driven approach outlined in this chapter is its modularity: each aspect can be useful on its own, and feed into wider analyses. The steps that got us to this stage included identifying short but car-dependent commuting routes (generated from desire lines) in Section 13.6 and analysis of route network characteristics with the sfnetworks package in Section 13.7. The final code chunk of this chapter combines these strands of analysis, by overlaying estimates of cycling potential from the previous section on top of a new dataset representing areas within a short distance of cycling infrastructure. This new dataset is created in the code chunk below which: 1) filters out the cycleway entities from the bristol_ways object representing the transport network; 2) ‘unions’ the individual LINESTRING entities of the cycleways into a single multilinestring object (for speed of buffering); and 3) creates a 100 m buffer around them to create a polygon.

existing_cycleways_buffer = bristol_ways |> 
  filter(highway == "cycleway") |>    # 1) filter out cycleways
  st_union() |>                       # 2) unite geometries
  st_buffer(dist = 100)               # 3) create buffer

The next stage is to create a dataset representing points on the network where there is high cycling potential but little provision for cycling.

route_network_no_infra = st_difference(
  route_network_scenario,
  route_network_scenario |> st_set_crs(st_crs(existing_cycleways_buffer)),
  existing_cycleways_buffer
)

The results of the preceding code chunks are shown in Figure 13.8, which shows routes with high levels of car dependency and high cycling potential but no cycleways.

tmap_mode("view")
qtm(route_network_no_infra, basemaps = leaflet::providers$Esri.WorldTopoMap,
    lines.lwd = 5)

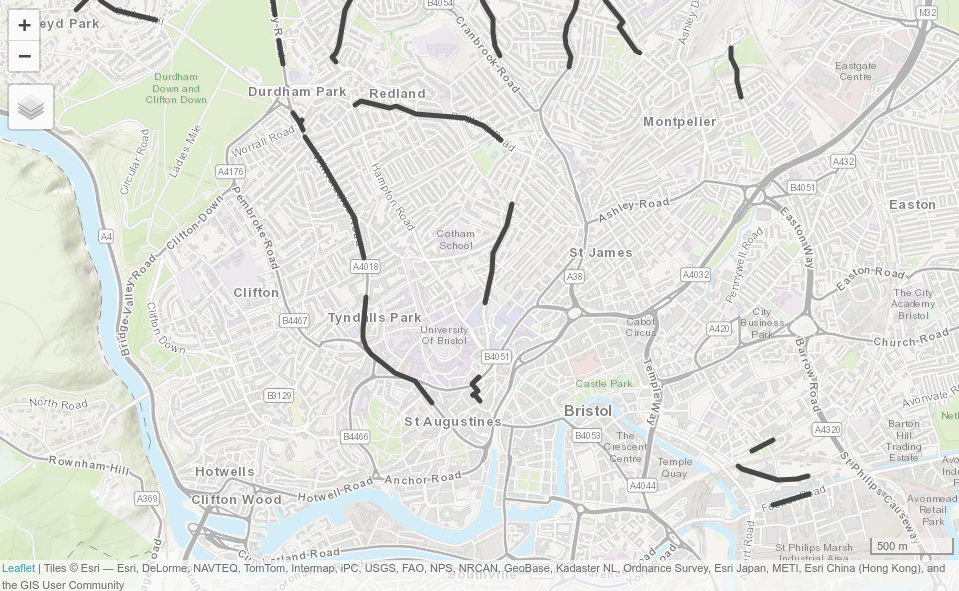
FIGURE 13.8: Potential routes along which to prioritise cycle infrastructure in Bristol to reduce car dependency. The static map provides an overview of the overlay between existing infrastructure and routes with high car-bike switching potential (left). The screenshot the interactive map generated from the qtm() function highlights Whiteladies Road as somewhere that would benefit from a new cycleway (right).

The method has some limitations: in reality, people do not travel to zone centroids or always use the shortest route algorithm for a particular mode. However, the results demonstrate how geographic data analysis can be used to highlight places where new investment in cycleways could be particularly beneficial, despite the simplicity of the approach. The analysis would need to be substantially expanded — including with larger input datasets — to inform transport planning design in practice.

13.9 Future directions of travel

This chapter provided a taste of the possibilities of using geocomputation for transport research, and explored some key geographic elements that make-up a city’s transport system with open data and reproducible code. The results could help plan where investment is needed.

Transport systems operate at multiple interacting levels, meaning that geocomputational methods have great potential to generate insights into how they work, and the likely impacts of different interventions. There is much more that could be done in this area: it would be possible to build on the foundations presented in this chapter in many directions. Transport is the fastest growing source of greenhouse gas emissions in many countries, and is set to become “the largest GHG emitting sector, especially in developed countries” (see EURACTIV.com). Transport-related emissions are unequally distributed across society but (unlike food and heating) are not essential for well-being. There is great potential for the sector to rapidly decarbonize through demand reduction, electrification of the vehicle fleet and the uptake of active travel modes such as walking and cycling. New technologies can reduce car dependency by enabling more car sharing. ‘Micro-mobility’ systems such as dockless bike and e-scooter schemes are also emerging, creating valuable datasets in the General Bikeshare Feed Specification (GBFS) format, which can be imported and processed with the gbfs package. These and other changes will have large impacts on accessibility, the ability of people to reach employment and service locations that they need, something that can be quantified currently and under scenarios of change with packages such as accessibility packages. Further exploration of such ‘transport futures’ at local, regional and national levels could yield important new insights.

Methodologically, the foundations presented in this chapter could be extended by including more variables in the analysis. Characteristics of the route such as speed limits, busyness and the provision of protected cycling and walking paths could be linked to ‘mode-split’ (the proportion of trips made by different modes of transport). By aggregating OpenStreetMap data using buffers and geographic data methods presented in Chapters 3 and 4, for example, it would be possible to detect the presence of green space in close proximity to transport routes. Using R’s statistical modeling capabilities, this could then be used to predict current and future levels of cycling, for example.

This type of analysis underlies the Propensity to Cycle Tool (PCT), a publicly accessible (see www.pct.bike) mapping tool developed in R that is being used to prioritize investment in cycling across England (Lovelace et al. 2017). Similar tools could be used to encourage evidence-based transport policies related to other topics such as air pollution and public transport access around the world.

13.10 Exercises

E1. In much of the analysis presented in the chapter we focused on active modes, but what about driving trips?

• What proportion of trips in the desire_lines object are made by driving?
• What proportion of desire_lines have a straight line length of 5 km or more in distance?
• What proportion of trips in desire lines that are longer than 5 km in length are made by driving?
• Plot the desire lines that are both less than 5 km in length and along which more than 50% of trips are made by car.
• What do you notice about the location of these car dependent yet short desire lines?

E2. What additional length of cycleways would result if all the routes presented in the last Figure, on sections beyond 100 m from existing cycleways, were constructed?

E3. What proportion of trips represented in the desire_lines are accounted for in the routes_short_scenario object?

• Bonus: what proportion of all trips happen on desire lines that cross routes_short_scenario?

E4. The analysis presented in this chapter is designed for teaching how geocomputation methods can be applied to transport research. If you were doing this for real, in government or for a transport consultancy, what top 3 things would you do differently?

E5. Clearly, the routes identified in the last Figure only provide part of the picture. How would you extend the analysis?

E6. Imagine that you want to extend the scenario by creating key areas (not routes) for investment in place-based cycling policies such as car-free zones, cycle parking points and reduced car parking strategy. How could raster datasets assist with this work?

• Bonus: develop a raster layer that divides the Bristol region into 100 cells (10 by 10) and estimate the average speed limit of roads in each, from the bristol_ways dataset (see Chapter 14).